August 17, 2018 Tagged: Clojure, Algorithms, Software
A* is a dead-simple path finding algorithm that, with a few tweaks, can be used to lazily generate a sequence of paths, shortest first.
I came across the necessity to implement it myself because the existing Clojure graph libraries (Loom, Ubergraph) are focused on finding the shortest path, whereas I wanted a lazy sequence of shortest paths.
(Note that if you’re looking for an optimal solution and don’t need A*’s heuristic, Yen’s algorithm is a good place to start. Also it’s cool because it’s something of a higher-order algorithm.)
A* is essentially a depth first search that chooses the adjacent node that we deem most likely to be the correct path to search first, so it’s easy to modify to then choose the second most likely node, etc. until we’ve lazily found an ordered sequence of shortest paths.
 |
Luckily Clojure, being a practical language, lends itself to a clear implementation. First we need to represent the graph:
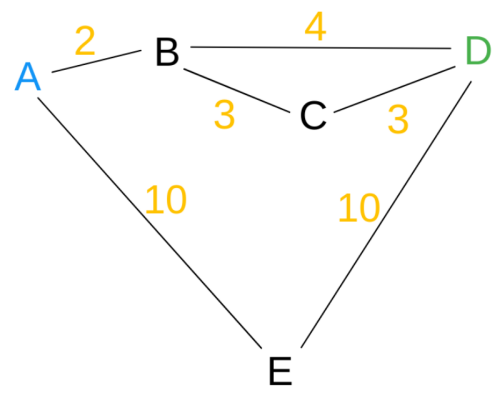
(def graph
"Map of node => set of adjacent nodes."
{"A" #{"B", "E"}
"B" #{"A", "C", "D"}
"C" #{"B", "D"}
"D" #{"B", "C", "E"}
"E" #{"A", "D"}})
(def costs
"Map of node => adjacent node => cost. This could
be replaced with any cost function of the shape
(node, node') => cost."
{"A" {"B" 2, "E" 10}
"B" {"A" 2, "C" 3, "D" 4}
"C" {"B" 3, "D" 2}
"D" {"B" 4, "C" 3, "E" 10}
"E" {"A" 10, "D" 10}})
We’ll represent each step from a parent node to a child node with a map of the format {:node _, :parent _, :cost _, :insertion _}. We keep track of insertion order because Clojure’s sorted set won’t default
to this tie-breaker. Given the step format, we write functions to generate a path from some step to its source and to compare steps:
(defn rpath [{:keys [node parent]}]
(lazy-seq
(cons node (when parent (rpath parent)))))
(defn cmp-step [step-a step-b]
(let [cmp (compare (:cost step-a) (:cost step-b))]
(if (zero? cmp)
(compare (:entered step-a) (:entered step-b))
cmp)))
A* determines the probable distance between some node & the destination with a heuristic function, whose only constraint is that it cannot overestimate the distance. We thus use a mock heuristic function which always returns zero (swap this out with your own heuristic) and a cost function that uses our map.
(def heuristic
(constantly 0))
(defn cost [node node']
(get-in costs [node node']))
There’s pseudocode on Wikipedia for A*, but I’ll put a slightly more concise version here for anyone blinded by Lisp’s parenthesis in my implementation:
fn a*
given graph, destination, adjacent_nodes
let node = first(adjacent_nodes) # Define first as least costly, using our cmp-step fn
let path = path_to_start(node) # Our rpath function
let adjacent_nodes' = remove(adjacent_nodes, node)
if node is dest
return (reverse(path), adjacent_nodes)
else
let unseen = fn node': not(in(path, node'))
let unseen_neighbors = filter(unseen, get(graph, node))
let as_steps = map(build_step(node, unseen_neighbors)) # build_step uses our cost fn
# Recur with new definitions, adding new adjacent nodes
a* graph = graph,
destination = destination,
adjacent_nodes = insert(adjacent_nodes', as_steps)
The above returns the tuple (shortest path, adjacent_nodes). To get the next shortest path, we need to pass in the modified adjacent_nodes structure and keep iterating calls to a* with that structure. Each subsequent call will return the next shortest path.
Translating to Clojure, we get:
(defn unseen? [path node]
(not-any? #{node} path))
(defn step-factory [parent last-insertion cost heur dest]
(fn [insertion-idx node]
{:parent parent
:node node
:entered (+ last-insertion (inc insertion-idx))
:cost (+ (:cost parent) (cost (:node parent) node) (heur node dest))}))
(defn next-a*-path [graph dest adjacent f-cost f-heur]
(when-let [{:keys [node] :as current} (first adjacent)]
(let [path (rpath current)
adjacent' (disj adjacent current)] ;; "pop" the current node
(if (= node dest)
[(reverse path), adjacent']
(let [last-idx (or (:entered (last adjacent')) 0)
factory (step-factory current last-idx f-cost f-heur dest)
xform (comp (filter (partial unseen? path)) (map-indexed factory))
adjacent'' (into adjacent' xform (get graph node))]
(recur graph dest adjacent'' f-cost f-heur))))))
To make something useful of this, we iterate calls to this function lazily. The full implementation becomes:
(declare a*-seq, next-a*-path, unseen?, step-factory, rpath, cmp-step)
(defn a*
"A sequence of paths from `src` to `dest`, shortest first, within the supplied `graph`.
If the graph is weighted, supply a `distance` function. To make use of A*, supply a
heuristic function. Otherwise performs like Dijkstra's algorithm."
[graph src dest & {:keys [distance heuristic]}]
(let [init-adjacent (sorted-set-by cmp-step {:node src :cost 0 :entered 0})]
(a*-seq graph dest init-adjacent
(or distance (constantly 1))
(or heuristic (constantly 0)))))
(defn a*-seq
"Construct a lazy sequence of calls to `next-a*-path`, returning the shortest path first."
[graph dest adjacent distance heuristic]
(lazy-seq
(when-let [[path, adjacent'] (next-a*-path graph dest adjacent distance heuristic)]
(cons path (a*-seq graph dest adjacent' distance heuristic)))))
(defn next-a*-path [graph dest adjacent f-cost f-heur]
(when-let [{:keys [node] :as current} (first adjacent)]
(let [path (rpath current)
adjacent' (disj adjacent current)] ;; "pop" the current node
(if (= node dest)
[(reverse path), adjacent']
(let [last-idx (or (:entered (last adjacent')) 0)
factory (step-factory current last-idx f-cost f-heur dest)
xform (comp (filter (partial unseen? path)) (map-indexed factory))
adjacent'' (into adjacent' xform (get graph node))]
(recur graph dest adjacent'' f-cost f-heur))))))
(defn unseen? [path node]
(not-any? #{node} path))
(defn step-factory [parent last-insertion cost heur dest]
(fn [insertion-idx node]
{:parent parent
:node node
:entered (+ last-insertion (inc insertion-idx))
:cost (+ (:cost parent) (cost (:node parent) node) (heur node dest))}))
(defn rpath [{:keys [node parent]}]
(lazy-seq
(cons node (when parent (rpath parent)))))
(defn cmp-step [step-a step-b]
(let [cmp (compare (:cost step-a) (:cost step-b))]
(if (zero? cmp)
(compare (:entered step-a) (:entered step-b))
cmp)))
Now we can run it:
;; Without a cost function, we get the shortest number of steps
(a* graph "A" "D")
; => (("A" "E" "D") ("A" "B" "D") ("A" "B" "C" "D"))
;; With a cost function...
(a* graph "A" "D" :distance cost)
; => (("A" "B" "D") ("A" "B" "C" "D") ("A" "E" "D"))
