I was putting together a Clojure library for RFC 6979’s deterministic elliptic curve digital signature algorithm (ECDSA) [1] on top of the JVM’s cryptographic primitives, and decided to try writing out ECDSA from scratch — separately from the production library! obviously — just to better understand what was going on with the deterministic k parameter that I was generating.

I got to step 6 of the algorithm described on the Wikipedia page before running out of vocabulary to Google the math that I needed to implement.

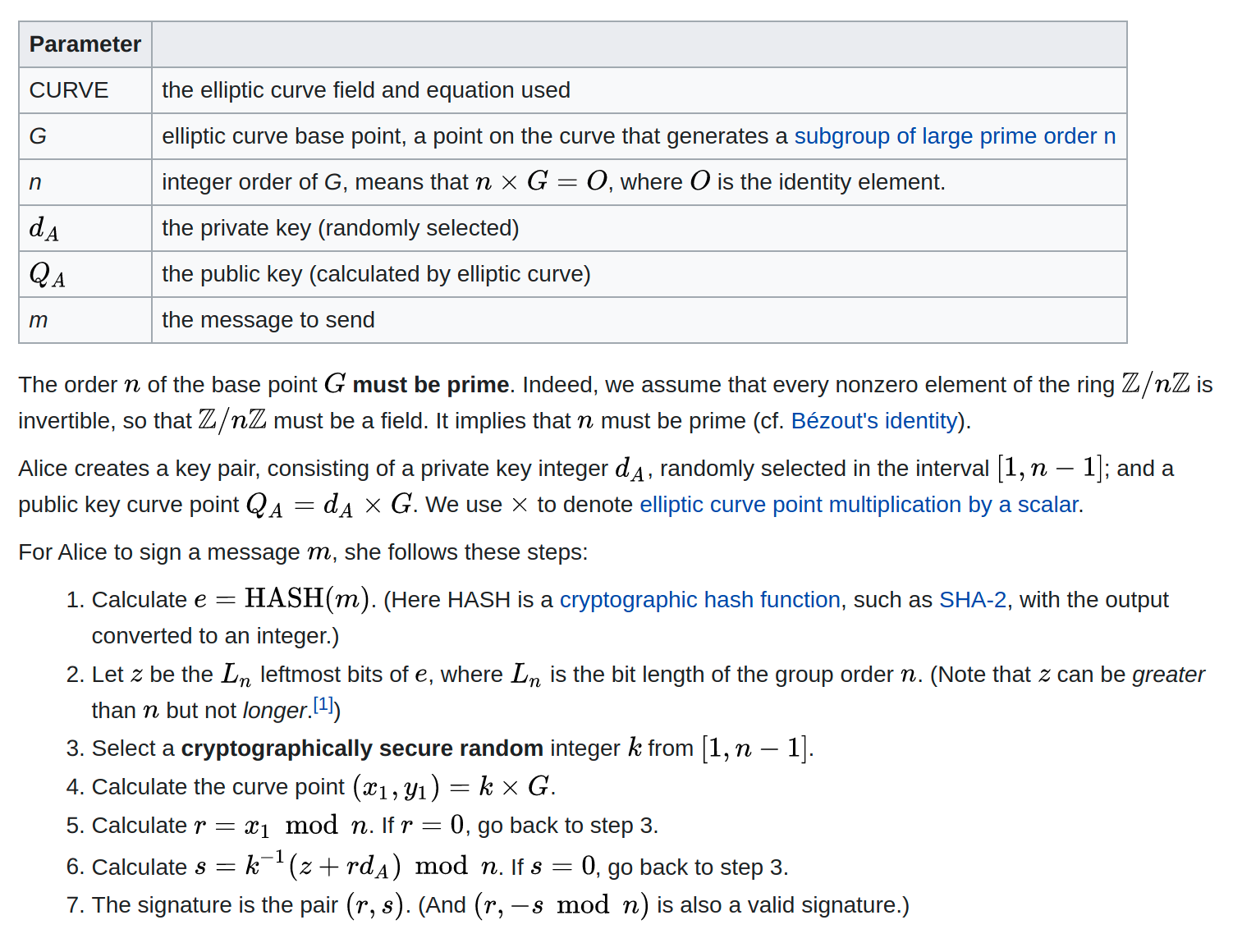
It is a modular multiplicative inverse. If it were s = k^-1 mod n it would be straightforward enough to Google ‘mod inverse’, but there’s an extra step.

s = k^-1 * x (mod n)
  = (k mod^-1 n) * x (mod n)

It’s actually clearer in code I think.

(defn modular-multiplicative-inverse
  "Find x in [0, p) such that (m * x) % p = n"
  [n m p]
  (let [n (biginteger n)
        m (biginteger m)
        p (biginteger p)] 
    (-> (.modInverse m p) 
        (.multiply n) 
        (.mod p))))